We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Systems of Nonlinear Equations and Inequalities

Halley’s Comet orbits the sun about once every 75 years. Its path can be considered to be a very elongated ellipse. Other comets follow similar paths in space. These orbital paths can be studied using systems of equations. These systems, however, are different from the ones we considered in the previous section because the equations are not linear.
A comet streaking across a starry sky. Halley’s Comet (credit: "NASA Blueshift"/Flickr)
In this section, we will consider the intersection of a parabola and a line, a circle and a line, and a circle and an ellipse. The methods for solving systems of nonlinear equations are similar to those for linear equations.

Graph Nonlinear Inequalities and Systems of Nonlinear Inequalities

All of the equations in the systems that we have encountered so far have involved equalities, but we may also encounter systems that involve inequalities. We have already learned to graph linear inequalities by graphing the corresponding equation, and then shading the region represented by the inequality symbol. As a reminder, here is one to try.  Choose the type of line first, then graph it, and click on the side that satisfies the inequality. Now, we will follow similar steps to graph a nonlinear inequality so that we can learn to solve systems of nonlinear inequalities. A nonlinear inequality is an inequality containing a nonlinear expression. Graphing a nonlinear inequality is much like graphing a linear inequality. Recall that when the inequality is greater than, [latex]y>a[/latex], or less than, [latex]y<a,\text{}[/latex] the graph is drawn with a dashed line. When the inequality is greater than or equal to, [latex]y\ge a,\text{}[/latex] or less than or equal to, [latex]y\le a,\text{}[/latex] the graph is drawn with a solid line. The graphs will create regions in the plane, and we will test each region for a solution. If one point in the region works, the whole region works. That is the region we shade.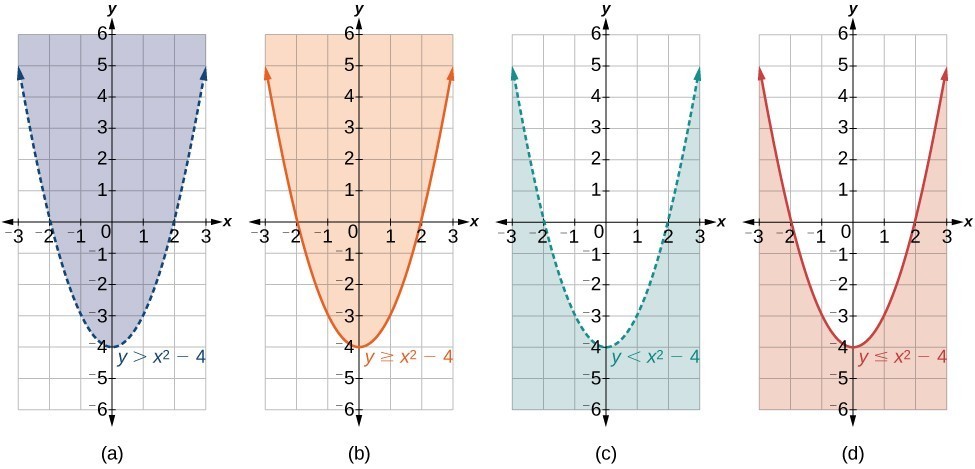
Four parabolas. For y greater than x squared minus 4 the parabola is dotted, and the region above the parabola is shaded. For y greater than or equal to x squared minus 4 the parabola is solid, and the region above it is shaded. For y less than x squared minus 4 the parabola is dotted, and the region below it is shaded. For y less than or equal to x squared minus 4 the parabola is solid, and the region below it is shaded. (a) an example of [latex]y>a[/latex]; (b) an example of [latex]y\ge a[/latex]; (c) an example of [latex]y<a[/latex]; (d) an example of [latex]y\le a[/latex]

How To: Given an inequality bounded by a parabola, sketch a graph.

  1. Graph the parabola as if it were an equation. This is the boundary for the region that is the solution set.
  2. If the boundary is included in the region (the operator is [latex]\le [/latex] or [latex]\ge [/latex] ), the parabola is graphed as a solid line.
  3. If the boundary is not included in the region (the operator is < or >), the parabola is graphed as a dashed line.
  4. Test a point in one of the regions to determine whether it satisfies the inequality statement. If the statement is true, the solution set is the region including the point. If the statement is false, the solution set is the region on the other side of the boundary line.
  5. Shade the region representing the solution set.

Example: Graphing an Inequality for a Parabola

Graph the inequality [latex]y>{x}^{2}+1[/latex].

Answer: First, graph the corresponding equation [latex]y={x}^{2}+1[/latex]. Since [latex]y>{x}^{2}+1[/latex] has a greater than symbol, we draw the graph with a dashed line. Then we choose points to test both inside and outside the parabola. Let’s test the points [latex]\left(0,2\right)[/latex] and [latex]\left(2,0\right)[/latex]. One point is clearly inside the parabola and the other point is clearly outside.

[latex]\begin{array}{ll}y>{x}^{2}+1\hfill & \hfill \\ 2>{\left(0\right)}^{2}+1\hfill & \hfill \\ 2>1\hfill & \text{True}\hfill \\ \hfill & \hfill \\ \hfill & \hfill \\ \hfill & \hfill \\ 0>{\left(2\right)}^{2}+1\hfill & \hfill \\ 0>5\hfill & \text{False}\hfill \end{array}[/latex]

The graph is shown below. We can see that the solution set consists of all points inside the parabola, but not on the graph itself.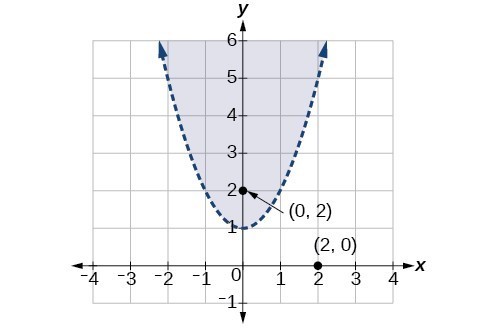 A dotted parabola with the region above it shaded. The point 0,2 is within the shaded region. The point 2,0 is not within the shaded region.

Graphing a System of Nonlinear Inequalities

Now that we have learned to graph nonlinear inequalities, we can learn how to graph systems of nonlinear inequalities. A system of nonlinear inequalities is a system of two or more inequalities in two or more variables containing at least one inequality that is not linear. Graphing a system of nonlinear inequalities is similar to graphing a system of linear inequalities. The difference is that our graph may result in more shaded regions that represent a solution than we find in a system of linear inequalities. The solution to a nonlinear system of inequalities is the region of the graph where the shaded regions of the graph of each inequality overlap, or where the regions intersect, called the feasible region.

How To: Given a system of nonlinear inequalities, sketch a graph.

  1. Find the intersection points by solving the corresponding system of nonlinear equations.
  2. Graph the nonlinear equations.
  3. Find the shaded regions of each inequality.
  4. Identify the feasible region as the intersection of the shaded regions of each inequality or the set of points common to each inequality.

Example: Graphing a System of Inequalities

Graph the given system of inequalities.

[latex]\begin{array}{r}\hfill {x}^{2}-y\le 0\\ \hfill 2{x}^{2}+y\le 12\end{array}[/latex]

Answer: These two equations are clearly parabolas. We can find the points of intersection by the elimination process: Add both equations and the variable [latex]y[/latex] will be eliminated. Then we solve for [latex]x[/latex].

[latex]\begin{array}\hfill x^{2}−y=0 \\ 2x^{2}+y=12 \\ \text{___________} \\ 3x^{2}=12 \\ x^{2}=4 \\ x=\pm 2\end{array}[/latex]

Substitute the x-values into one of the equations and solve for [latex]y[/latex].

[latex]\begin{array}{r}\hfill {x}^{2}-y=0\\ \hfill {\left(2\right)}^{2}-y=0\\ \hfill 4-y=0\\ \hfill y=4\\ \hfill \\ \hfill {\left(-2\right)}^{2}-y=0\\ \hfill 4-y=0\\ \hfill y=4\end{array}[/latex]

The two points of intersection are [latex]\left(2,4\right)[/latex] and [latex]\left(-2,4\right)[/latex]. Notice that the equations can be rewritten as follows.

[latex]\begin{array}{l}{x}^{2}-y\le 0\hfill \\ {x}^{2}\le y\hfill \\ y\ge {x}^{2}\hfill \\ \hfill \\ 2{x}^{2}+y\le 12\hfill \\ y\le -2{x}^{2}+12\hfill \end{array}[/latex]

Graph each inequality. The feasible region is the region between the two equations bounded by [latex]2{x}^{2}+y\le 12[/latex] on the top and [latex]{x}^{2}-y\le 0[/latex] on the bottom.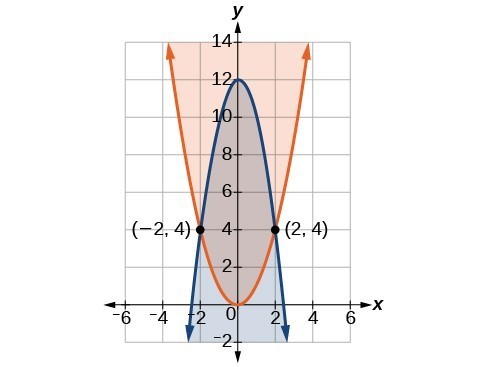 Two parabolas that intersect at the points negative 2, four and two, four. The region above the orange parabola is shaded, and the region below the blue parabola is shaded.

Try It

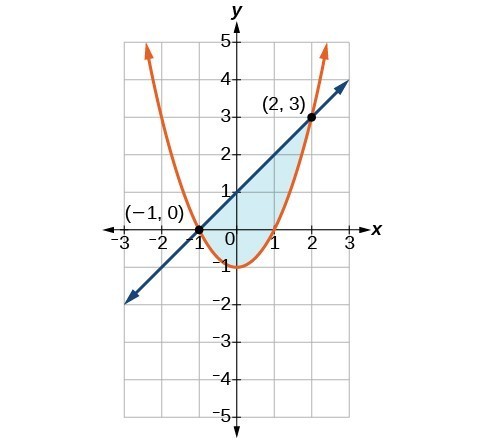
Graph the given system of inequalities.

[latex]\begin{array}{l}\text{ }y\ge {x}^{2}-1\hfill \\ x-y\ge -1\hfill \end{array}[/latex]

Answer: Shade the area bounded by the two curves, above the quadratic and below the line. A line intersecting a parabola at the points negative one, zero and two, three. The region under the line but above the parabola is shaded.

Try it

Use the sliders in the graph below to find equations for lines that produce systems with the following types of solutions:
  • One solution
  • Two solutions
  • No solutions
https://www.desmos.com/calculator/yq47tetslx
 

Intersection of a Circle and a Line

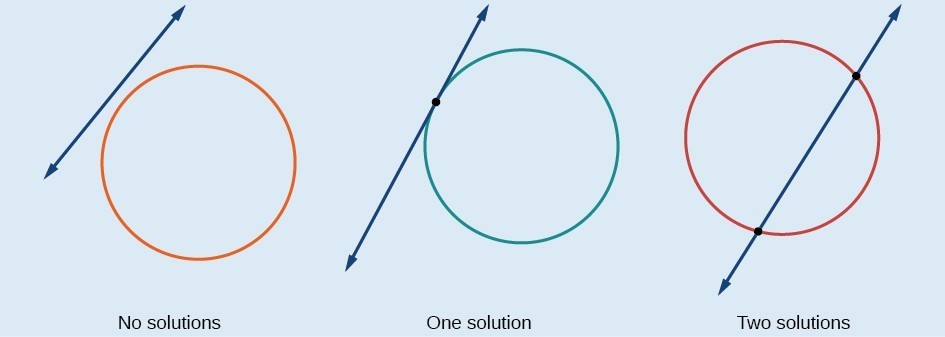
Just as with a parabola and a line, there are three possible outcomes when solving a system of equations representing a circle and a line.

A General Note: Possible Types of Solutions for the Points of Intersection of a Circle and a Line

The graph below illustrates possible solution sets for a system of equations involving a circle and a line.
  • No solution. The line does not intersect the circle.
  • One solution. The line is tangent to the circle and intersects the circle at exactly one point.
  • Two solutions. The line crosses the circle and intersects it at two points.
Image described in main body

How To: Given a system of equations containing a line and a circle, find the solution.

  1. Solve the linear equation for one of the variables.
  2. Substitute the expression obtained in step one into the equation for the circle.
  3. Solve for the remaining variable.
  4. Check your solutions in both equations.

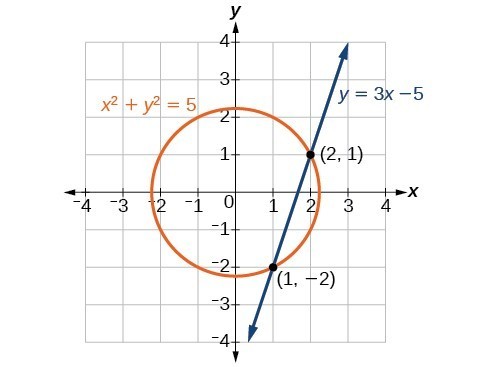
Example: Finding the Intersection of a Circle and a Line by Substitution

Find the intersection of the given circle and the given line by substitution.
[latex]\begin{array}{l}{x}^{2}+{y}^{2}=5\hfill \\ y=3x - 5\hfill \end{array}[/latex]

Answer: One of the equations has already been solved for [latex]y[/latex]. We will substitute [latex]y=3x - 5[/latex] into the equation for the circle.

[latex]\begin{array}{c}{x}^{2}+{\left(3x - 5\right)}^{2}=5\\ {x}^{2}+9{x}^{2}-30x+25=5\\ 10{x}^{2}-30x+20=0\end{array}[/latex]
Now, we factor and solve for [latex]x[/latex].
[latex]\begin{array}{l}10\left({x}^{2}-3x+2\right)=0\hfill \\ 10\left(x - 2\right)\left(x - 1\right)=0\hfill \\ x=2\hfill \\ x=1\hfill \end{array}[/latex]
Substitute the two x-values into the original linear equation to solve for [latex]y[/latex].
[latex]\begin{array}{l}y=3\left(2\right)-5\hfill \\ =1\hfill \\ y=3\left(1\right)-5\hfill \\ =-2\hfill \end{array}[/latex]
The line intersects the circle at [latex]\left(2,1\right)[/latex] and [latex]\left(1,-2\right)[/latex], which can be verified by substituting these [latex]\left(x,y\right)[/latex] values into both of the original equations. Line y equals 3x minus 5 crosses circle x squared plus y squared equals five at the points 2,1 and 1, negative 2.

Try It

Solve the system of nonlinear equations.
[latex]\begin{array}{l}{x}^{2}+{y}^{2}=10\hfill \\ x - 3y=-10\hfill \end{array}[/latex]

Answer: [latex]\left(-1,3\right)[/latex]

Solving a System of Nonlinear Equations Using Elimination

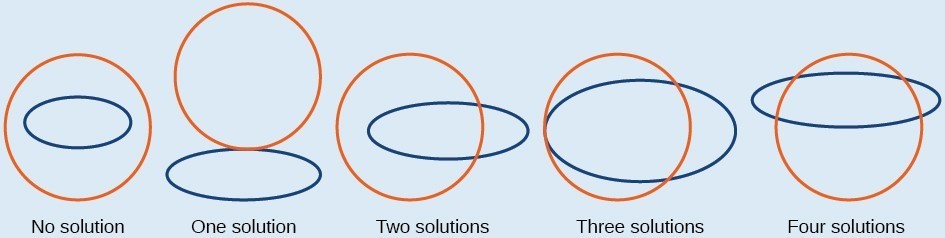
We have seen that substitution is often the preferred method when a system of equations includes a linear equation and a nonlinear equation. However, when both equations in the system have like variables of the second degree, solving them using elimination by addition is often easier than substitution. Generally, elimination is a far simpler method when the system involves only two equations in two variables (a two-by-two system), rather than a three-by-three system, as there are fewer steps. As an example, we will investigate the possible types of solutions when solving a system of equations representing a circle and an ellipse.

A General Note: Possible Types of Solutions for the Points of Intersection of a Circle and an Ellipse

The figure below illustrates possible solution sets for a system of equations involving a circle and an ellipse.
  • No solution. The circle and ellipse do not intersect. One shape is inside the other or the circle and the ellipse are a distance away from the other.
  • One solution. The circle and ellipse are tangent to each other, and intersect at exactly one point.
  • Two solutions. The circle and the ellipse intersect at two points.
  • Three solutions. The circle and the ellipse intersect at three points.
  • Four solutions. The circle and the ellipse intersect at four points.
Image described in main body

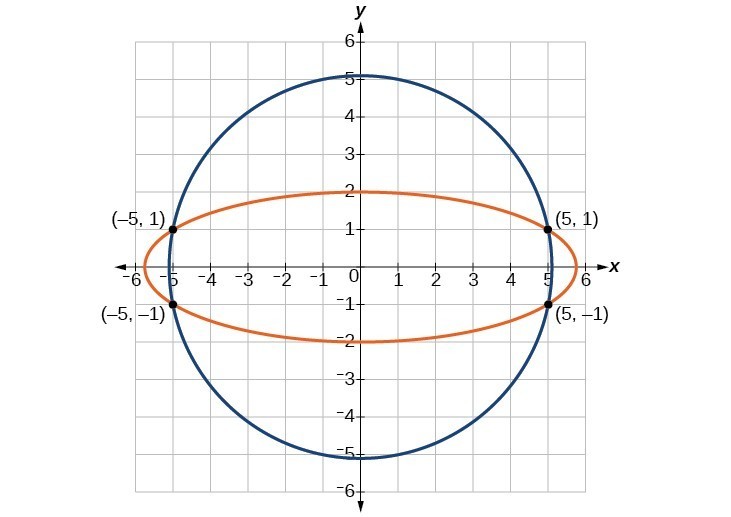
Example: Solving a System of Nonlinear Equations Representing a Circle and an Ellipse

Solve the system of nonlinear equations.
[latex]\begin{array}{rr}\hfill {x}^{2}+{y}^{2}=26& \hfill \left(1\right)\\ \hfill 3{x}^{2}+25{y}^{2}=100& \hfill \left(2\right)\end{array}[/latex]
 

Answer: Let’s begin by multiplying equation (1) by [latex]-3,\text{}[/latex] and adding it to equation (2).

[latex]\frac{\begin{array}{l}\begin{array}{l}\hfill \\ \left(-3\right)\left({x}^{2}+{y}^{2}\right)=\left(-3\right)\left(26\right)\hfill \\ \text{ }-3{x}^{2}-3{y}^{2}=-78\hfill \end{array}\hfill \\ \text{ }3{x}^{2}+25{y}^{2}=100\hfill \end{array}}{\text{ }22{y}^{2}=22}[/latex]
After we add the two equations together, we solve for [latex]y[/latex].
[latex]\begin{array}{l}{y}^{2}=1\hfill \\ y=\pm \sqrt{1}=\pm 1\hfill \end{array}[/latex]
Substitute [latex]y=\pm 1[/latex] into one of the equations and solve for [latex]x[/latex].
[latex]\begin{array}{l}\text{ }{x}^{2}+{\left(1\right)}^{2}=26\hfill \\ \text{ }{x}^{2}+1=26\hfill \\ \text{ }{x}^{2}=25\hfill \\ \text{ }x=\pm \sqrt{25}=\pm 5\hfill \\ \hfill \\ {x}^{2}+{\left(-1\right)}^{2}=26\hfill \\ \text{ }{x}^{2}+1=26\hfill \\ \text{ }{x}^{2}=25=\pm 5\hfill \end{array}[/latex]
There are four solutions:

[latex]\left(5,1\right),\left(-5,1\right),\left(5,-1\right),\text{and}\left(-5,-1\right)[/latex].

Circle intersected by ellipse at four points. Those points are negative five, one; five, one; five, negative one; and negative five, negative one.

Try It

Use Desmos to find the solution to the system of equations.
[latex]\begin{array}{c}4{x}^{2}+{y}^{2}=13\\ {x}^{2}+{y}^{2}=10\end{array}[/latex]

Answer: [latex]\left\{\left(1,3\right),\left(1,-3\right),\left(-1,3\right),\left(-1,-3\right)\right\}[/latex]

In the following video, we present an example of how to solve a system of non-linear equations that represent the intersection of an ellipse and a hyperbola. https://youtu.be/Ic-42kmdJqc

Key Concepts

  • There are three possible types of solutions to a system of equations representing a line and a parabola: (1) no solution, the line does not intersect the parabola; (2) one solution, the line is tangent to the parabola; and (3) two solutions, the line intersects the parabola in two points.
  • There are three possible types of solutions to a system of equations representing a circle and a line: (1) no solution, the line does not intersect the circle; (2) one solution, the line is tangent to the parabola; (3) two solutions, the line intersects the circle in two points.
  • There are five possible types of solutions to the system of nonlinear equations representing an ellipse and a circle: (1) no solution, the circle and the ellipse do not intersect; (2) one solution, the circle and the ellipse are tangent to each other; (3) two solutions, the circle and the ellipse intersect in two points; (4) three solutions, the circle and ellipse intersect in three places; (5) four solutions, the circle and the ellipse intersect in four points.
  • An inequality is graphed in much the same way as an equation, except for > or <, we draw a dashed line and shade the region containing the solution set.
  • Inequalities are solved the same way as equalities, but solutions to systems of inequalities must satisfy both inequalities.

Glossary

feasible region the solution to a system of nonlinear inequalities that is the region of the graph where the shaded regions of each inequality intersect nonlinear inequality an inequality containing a nonlinear expression system of nonlinear equations a system of equations containing at least one equation that is of degree larger than one system of nonlinear inequalities a system of two or more inequalities in two or more variables containing at least one inequality that is not linear

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 12575. Authored by: Alyson Day. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 70349. Authored by: Roy Shahbazian. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 19940. Authored by: Georgiakaki, Sophia. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question 65041. Authored by: Etgen, Benjamin. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 62704. Authored by: Hidegkuti, Marta. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 29703. Authored by: McClure, Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Ex 3: Solve a System of Nonlinear Equations (Elimination). Authored by: Sousa, James (Mathispower4u). License: CC BY: Attribution.

CC licensed content, Specific attribution